Data engines

From optimizing models to optimizing models and data

Our data engine

To create an image, raw sensor data traverses complex image signal processing pipelines. These pipelines are used by cameras and scientific instruments to produce the images fed into machine learning systems. The processing pipelines vary by device, influencing the resulting image statistics and ultimately contributing to what is known as hardware-drift. However, this processing is rarely considered in machine learning modelling, because available benchmark data sets are generally not in raw format. Here we show that pairing qualified raw sensor data with an explicit, differentiable model of the image processing pipeline allows to tackle camera hardware-drift. Specifically, we demonstrate (1) the controlled synthesis of metrologically accurate data, (2) data optimization, as well as (3) device-precise data quality control.

Click here for a walkthrough of sample raw optical data

Raw data

We make available two data sets. The first, Raw-Microscopy, contains 940 raw bright-field microscopy images of human blood smear slides for leukocyte classification alongside 5,640 variations measured at six different intensities and twelve additional sets totalling 11,280 images of the raw sensor data processed through different pipelines. The second, Raw-Drone, contains 548 raw drone camera images for car segmentation, alongside 3,288 variations measured at six different intensities and also twelve additional sets totalling 6,576 images of the raw sensor data processed through different pipelines.

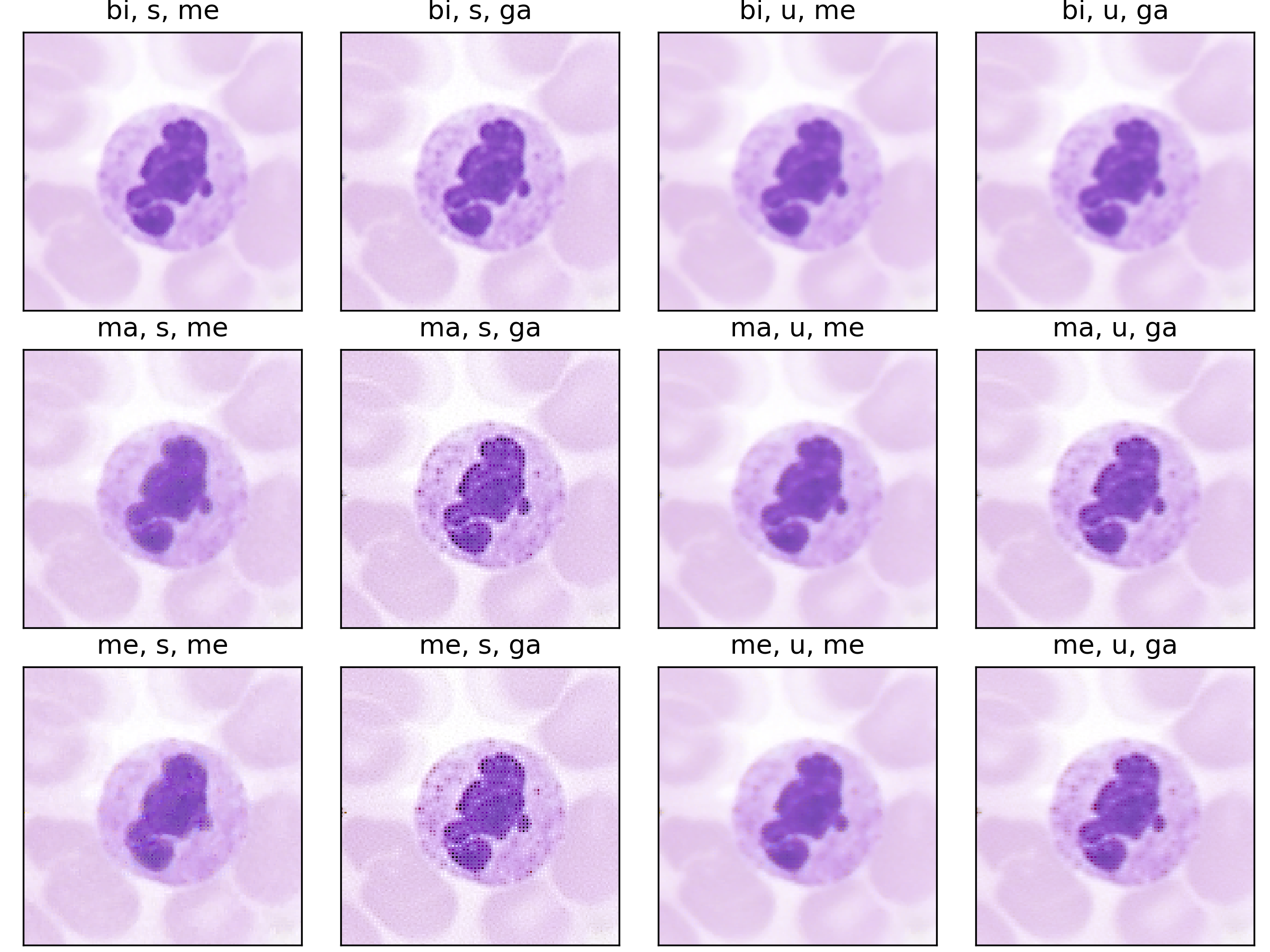
Raw-Microscopy

Assessment of blood smears under a light microscope is a key diagnostic technique . The creation of image datasets and machnine learning models on them has received wide interest in recent years . Here, we use a bright-field microscope to image blood smear cytopathology samples. The light source is a halogen lamp equipped with a 0.55 NA condenser, and a pre-centred field diaphragm unit. We use filters at 450 nm, 525 nm and 620 nm to acquire the blue, green and red channels respectively. The condenser is followed by a 40 \(\times\) objective with 0.95 NA (Olympus UPLXAPO40X). Slides can be moved via a piezo with 1 nm spatial resolution, in the three directions. We focus by maximizing the variance of the pixel values. Images are acquired is 16 bit, with a 2560 \(\times\) 2160 pixels CMOS sensor (PCO edge 5.5). We measured the PSF to be 450 nm with 100 nm nanospheres. Mechanical drift was measured at 0.4 pixels per hour. Imaging was performed on de-identified human blood smear slides (Ma190c Lieder, J. Lieder GmbH & Co. KG, Ludwigsburg/Germany). All slides were taken from healthy humans without known hematologic pathology. Imaging regions were selected to contain single leukoytes in order to allow unique labelling of image patches, and regions were cropped to 256 \(\times\) 256 pixels. All images were annotated by a trained hematological cytologist using the standard scheme of normal leukocytes comprising band and segmented neutrophils, typical and atypical lymphocytes, monocytes, eosinophils and basophils . To soften class imbalance, candidates for rare normal leukocyte types were preferentially imaged, and enrich rare classes. Additionally, two classes for debris and smudge cells, as well as cells of unclear morphology were included. Labelling took place for all imaged cells from a particular smear at a time, with single-cell patches shown in random order. RI are generated using JetRaw Data Suite features. Blue, red and green channels are metrologically rescaled independently in intensity to simulate a standard RGB camera condition. From each channel, some pixels are discarded complementary on each channel in order to obtain a Bayer filter pattern.

Raw-Drone

We used a DJI Mavic 2 Pro Drone, equipped with a Hasselblad L1D-20c camera (Sony IMX183 sensor) having 2.4 \(\micro\)m pixels in Bayer filter array. The objective has a focal length of 10.3 mm. We set the f-number \(N=8\), to emulate the PSF circle diameter relative to the pixel pitch and ground sampling distance (GSD) as would be found on images from high-resolution satellites. The point-spread function (PSF) was measured to have a circle diameter of 12.5\(\micro\)m. This corresponds to a diffraction-limited system, within the uncertainty dominated by the wavelength spread of the image. Images were taken at 200 ISO, a gain of 0.528 DN/\(e^-\). The 12-bit pixel values are however left-justified to 16-bits, so that the gain on the 16-bit numbers is 8.448 DN/$e^-$. The images were taken at a height of 250 m, so that the GSD is 6 cm. All images were tiled in 256 \(\times\) 256 patches. Segmentation color masks were created to identify cars for each patch. From this mask, classification labels were generated to detect if there is a car in the image. The dataset is constituted by 548 images for the segmentation task, and 930 for classification. The dataset is augmented through JetRaw Data Suite, with 7 different intensity scales.

Physical layer

Let \((X,Y):\Omega \to \mathbb{R}^{H,W}\times \mathcal{Y}\) be the raw sensor data generating random variable on some probability space \((\Omega, \mathcal{F},\mathbb{P})\), with \(\mathcal{Y}=\{0,1\}^{K}\) for classification and \(\mathcal{Y}=\{0,1\}^{H,W}\) for segmentation. Let \(\Phi_{Task}:\mathbb{R}^{C,H,W}\to\mathcal{Y}\) be the task model determined during training. The inputs that are given to the task model are the outputs of the image signal processing (ISP). We distinguish between the raw sensor image \(\boldsymbol{x}\) and a view \(\boldsymbol{v}\) of this image. In contrast to the classical setting, this approach is more sensitive to the origin of distribution shifts, as outlined in our formal companion.

The static pipeline

Following the most common steps in ISP, we define the static pipeline as the composition \(\begin{equation*} \Phi^{stat}_{Proc} := \Phi_{GC} \circ \Phi_{DN} \circ \Phi_{SH} \circ \Phi_{CC} \circ \Phi_{WB} \circ \Phi_{DM} \circ \Phi_{BL}, \end{equation*}\) mapping a raw sensor image to a RGB image. The static pipeline enables us to create (multiple) different views of the same raw sensor data by manually changing the configurations of the intermediate steps. Fixing the continuous features, but varying \(\Phi_{DM}\), \(\Phi_{SH}\) and \(\Phi_{DN}\) results in the twelve different views visible further down in this post. For a detailed description of the static pipeline and its intermediate steps we refer to our formal companion.

def get_b2_bucket():
    bucket_name = 'perturbed-minds'
    application_key_id = '003d6b042de536a0000000008'
    application_key = 'K003HMNxnoa91Dy9c0V8JVCKNUnwR9U'
    info = InMemoryAccountInfo()
    b2_api = B2Api(info)
    b2_api.authorize_account('production', application_key_id, application_key)
    bucket = b2_api.get_bucket_by_name(bucket_name)
    return bucket

python train.py \
    --experiment_name YOUR-EXPERIMENT-NAME \
    --run_name YOUR-RUN-NAME \
    --dataset Microscopy \
    --lr 1e-5 \
    --n_splits 5 \
    --epochs 5 \
    --classifier_pretrained \
    --processing_mode static \
    --augmentation weak \
    --log_model True \
    --iso 0.01 \
    --freeze_processor \
    --track_processing \
    --track_every_epoch \
    --track_predictions \
    --track_processing_gradients \
    --track_save_tensors \

The parametrized pipeline

For a fixed raw sensor image, the parametrized pipeline \(\Phi^{\theta}_{Proc}\) maps from a parameter space \(\Theta\) to a RGB image. The parametrized pipeline is differentiable wrt. the parameters in \(\boldsymbol{\theta}\). This enables us to backpropagate the gradient from the output of the task model through the ISP back to the raw sensor image. You can find more details in our formal companion.

Gradients (top row) and generated views (bottom row) over time for the parametrized pipeline in order (demosaicing, color correction, sharpening, denoising, gamma correction) on the Raw-Microscopy dataset with a downstream ResNet task model. Note that compression of the video files for faster online viewing creates artifacts. Original, uncompressed image files can be accessed through the virtual lab log.

Gradients (top row) and generated views (bottom row) over time for the parametrized pipeline in order (demosaicing, color correction, sharpening, denoising, gamma correction) on the Raw-Drone dataset with a downstream U-Net++ task model. Note that compression of the video files for faster online viewing creates artifacts. Original, uncompressed image files can be accessed through the virtual lab log.

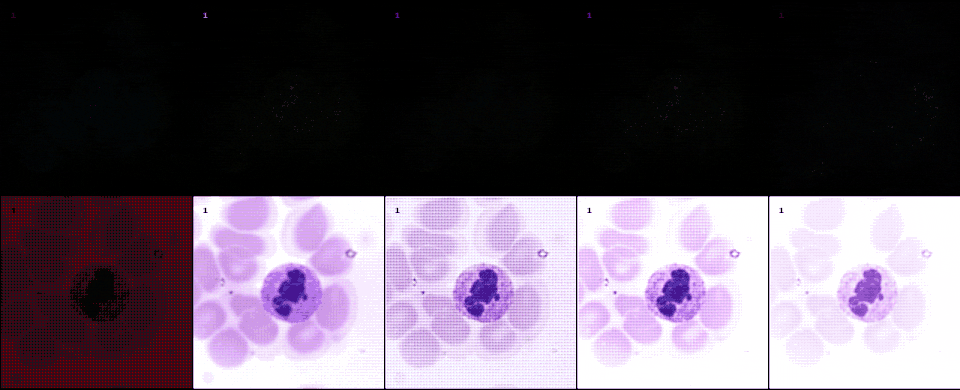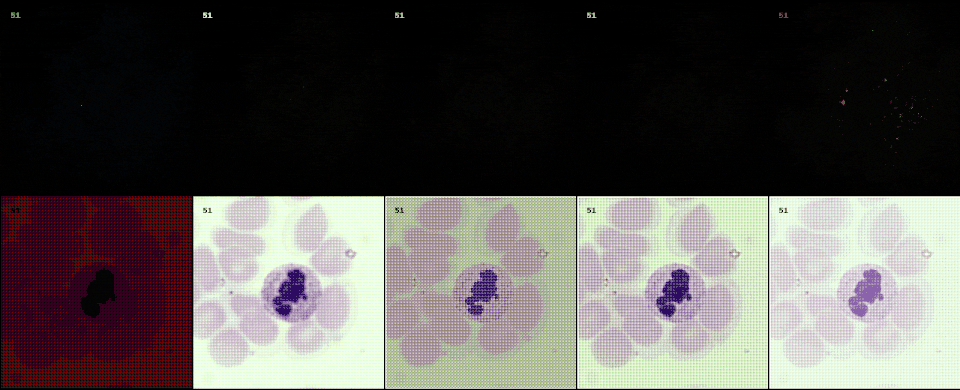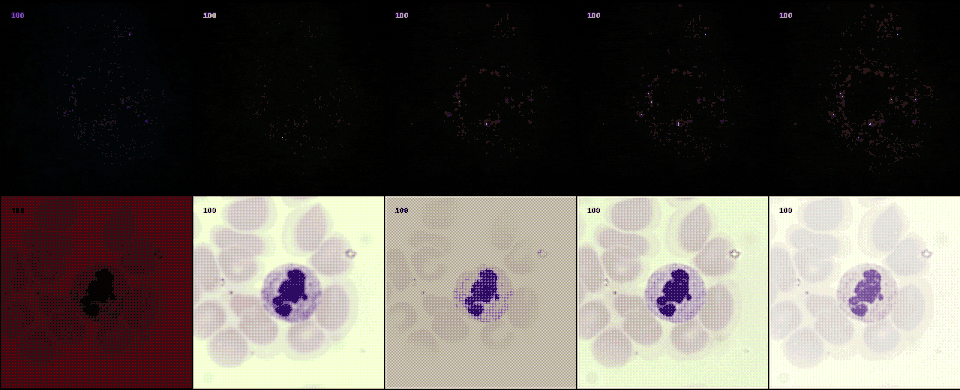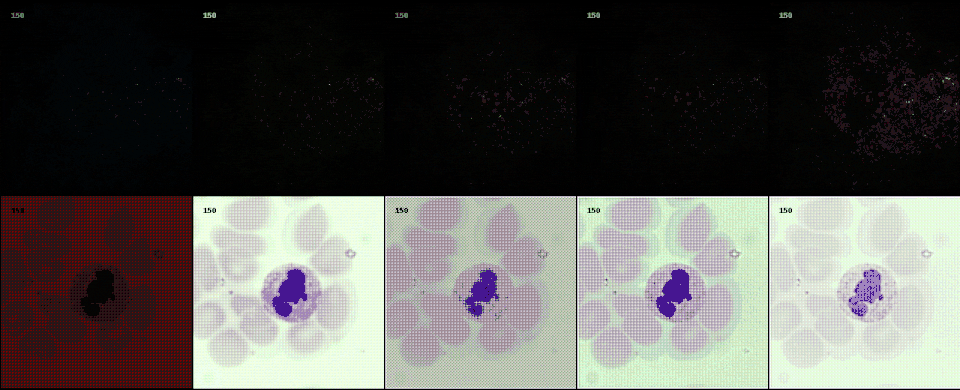
Semantic layer

The original scene from which an optical image is captured extends beyond the confines of acquisition data model. This semantic layer is captured by the semantic layer of our data engines. In this example from a project with collaborators at LMU and Aignostics, we employ a diffusion model to model to generate cell structures.

Use cases and benefits

With these data engines in our hands we are able to do interesting things. We can synthesize new data on demand (for example for training and testing), we can optimize existing data (for example to reduce hardware cost of acquisition devices) and we can monitor and control the quality of data (for example during deployment or for certification) to metrological precision.

Data synthesis

From one-to-many: bootstrap physical layer and one reference measurement to many metrologically precise synthetic data points. Save cost and acquistion time for training and testing of machine learning models.

Static processing variations on the Raw Microscopy dataset.

Static processing variations on the Raw Drone dataset.

Code example

python train.py \
    --experiment_name YOUR-EXPERIMENT-NAME \
    --run_name YOUR-RUN-NAME \
    --dataset Microscopy \
    --lr 1e-5 \
    --n_splits 5 \
    --epochs 5 \
    --classifier_pretrained \
    --processing_mode static \
    --augmentation weak \
    --log_model True \
    --iso 0.01 \
    --freeze_processor \
    --track_processing \
    --track_every_epoch \
    --track_predictions \
    --track_processing_gradients \
    --track_save_tensors \

From noise to structure: leverage the semantic layer to generate high fidelity scenes.

Diffusion model schematic from our machine learning in pathology project.

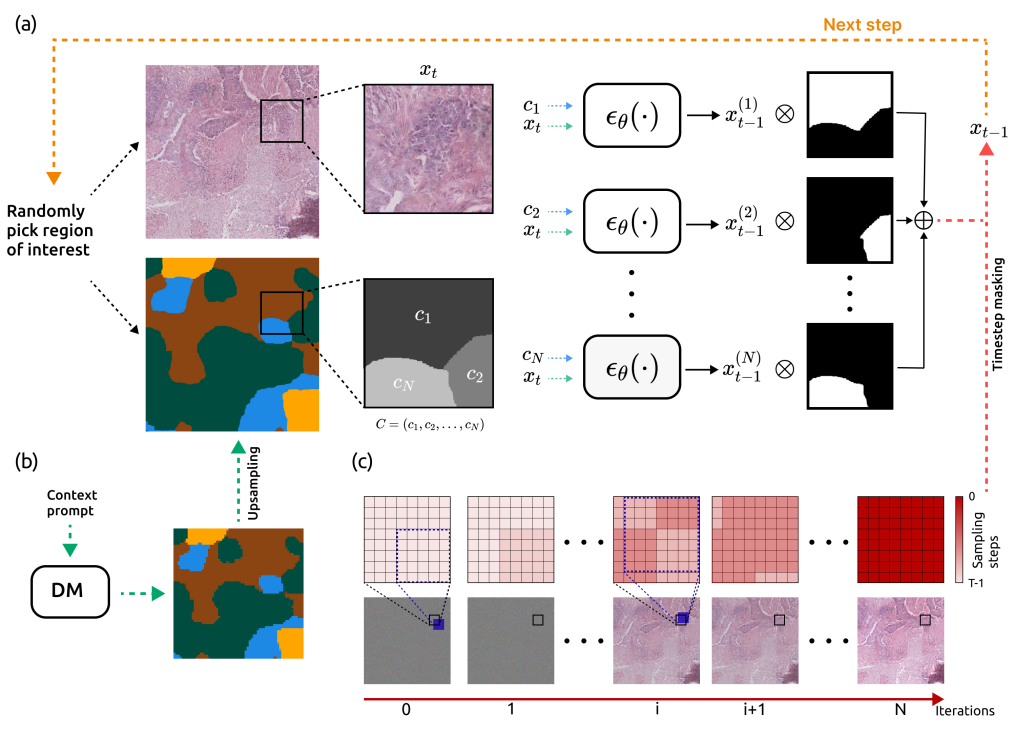
Data optimization

From data to machine optimal data: optimize data acquisition for downstream machine consumption. Improve training convergence, stability and performance, reduce hardware costs.

Data optimized jointly with the task model (learned) versus fixed data (frozen).

Code example

python train.py \
    --experiment_name YOUR-EXPERIMENT-NAME \
    --run_name YOUR-RUN-NAME \
    --dataset Microscopy \
    --lr 1e-5 \
    --n_splits 5 \
    --epochs 5 \
    --classifier_pretrained \
    --processing_mode parametrized \
    --augmentation weak \
    --log_model True \
    --iso 0.01 \
    --track_processing \
    --track_every_epoch \
    --track_predictions \
    --track_processing_gradients \
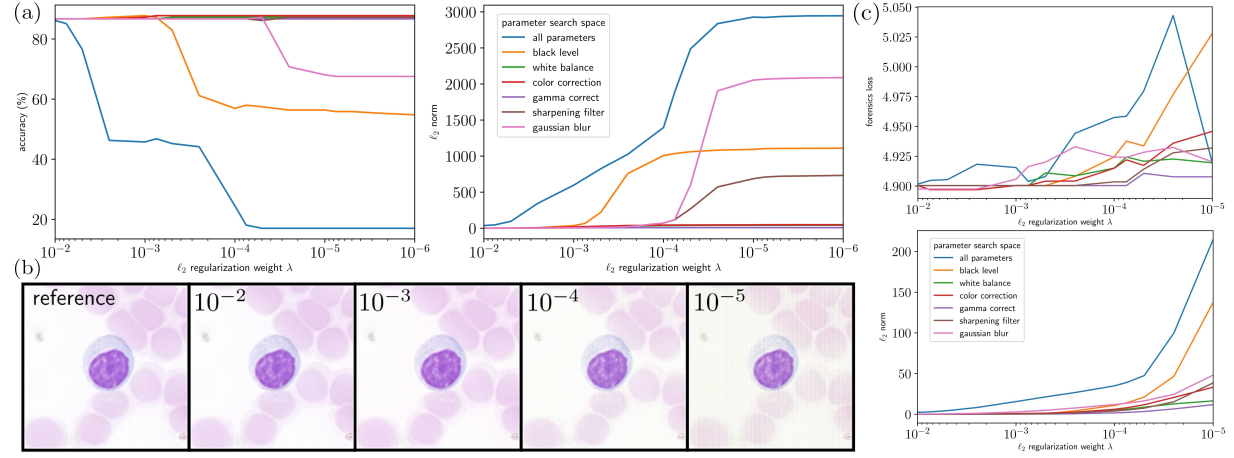
    --track_save_tensors \

Data quality control

From data to machine optimal data: optimize data acquisition for downstream machine consumption. Improve training convergence, stability and performance, reduce hardware costs.

Tolerancing forensic signatures for classification and segmentation models wrt variations in the data generating processes.

Code example

python train.py \
    --experiment_name YOUR-EXPERIMENT-NAME \
    --run_name YOUR-RUN-NAME \
    --dataset Microscopy \
    --adv_training
    --lr 1e-5 \
    --n_splits 5 \
    --epochs 5 \
    --classifier_pretrained \
    --processing_mode parametrized \
    --augmentation weak \
    --log_model True \
    --iso 0.01 \
    --track_processing \
    --track_every_epoch \
    --track_predictions \
    --track_processing_gradients \
    --track_save_tensors \

Resources

Data

Access

If you use our code you can use the convenient cloud storage integration. Data will be loaded automatically. We also maintain a copy of the entire dataset with a persistent and permanent identifier at Zenodo which you can find under identifier 10.5281/zenodo.5235536.

License

The demo data is published under a Attribution 4.0 International (CC BY 4.0) which allows liberal copying, redistribution, remixing and transformation. The authors bear all responsibility for the published data.

Code

Access

All demo code is available at the raw2logit repository.

License

The demo code is published under MIT license which permits broad commercial use, distribution, modification and private use.

Virtual lab log

We maintain a collaborative virtual lab log at this address. There you can browse experiment runs, analyze results through SQL queries and download trained processing and task models.

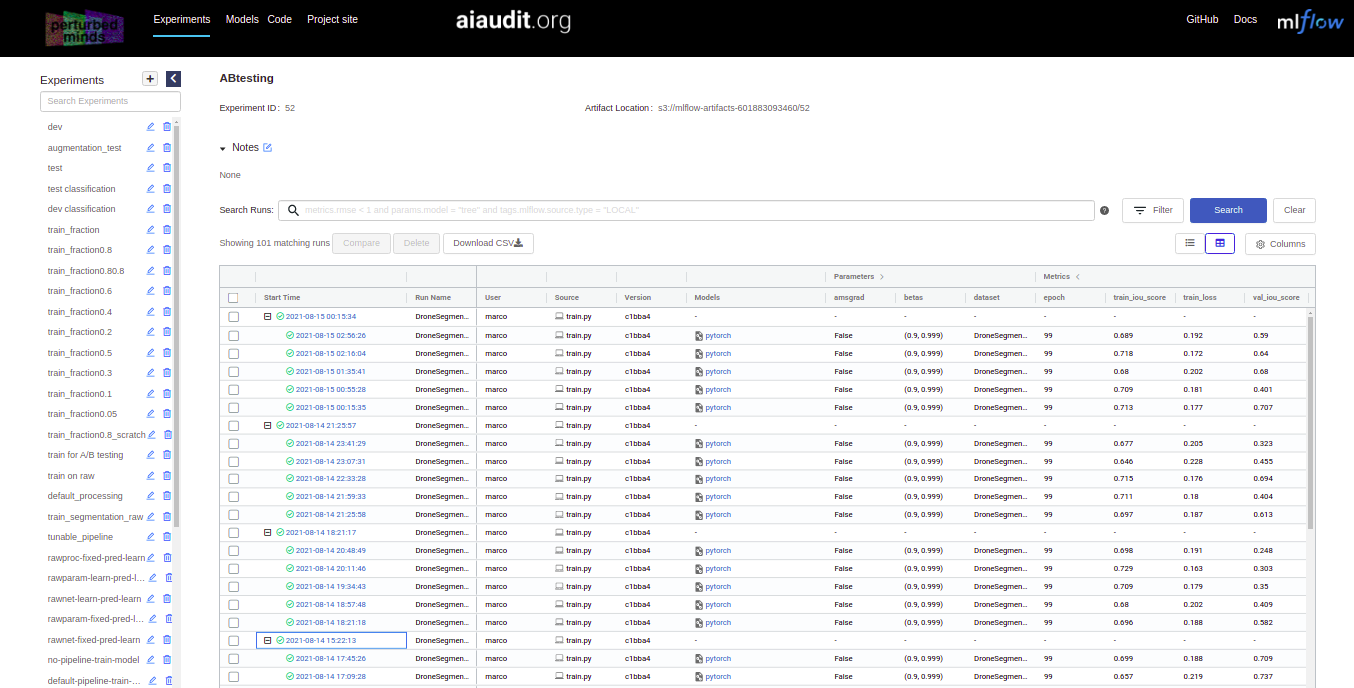
For better overview we include a map between the names of experiments in the paper and names of experiments in the virtual lab log:

Name of experiment in paper	Name of experiment in virtual lab log
Data synthesis	1 Controlled synthesis of hardware-drift test cases (Train) , 1 Controlled synthesis of hardware-drift test cases (Test)
Data optimization	3 Image processing customization (Microscopy), 3 Image processing customization (Drone)
Data QA	2 Modular hardware-drift forensics

Note that the virtual lab log includes many additional experiments.

To reference this material use

@book{2ml2023,
  title      = {Metrological machine learning (2ML)},
  author     = {Luis Oala},
  year       = {2023},
  edition    = {1},
  url        = {https://metrological.ml}
}